STRUCTURES - SUPPORT SYMBOLS

The diagrams show common types of support at left and related symbols at right.  In  addition to the pin and roller support described above, they also include fixed-end  support (as used in steel and concrete moment frames, for example).

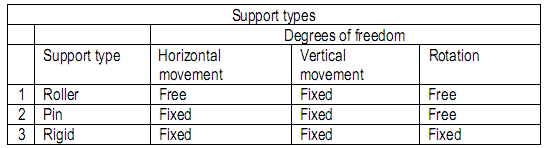
SUPPORTS TYPES - STRUCTURES

For convenience, support types are described  for beams, but apply to other horizontal  elements, like trusses, as well.  The type of support affects analysis and design, as well  as performance.  Given the three equations of statics defined above, ΣH=0, ΣV=0, and  ΣM=0, beams with three unknown reactions are considered determinate  (as described  below) and can be analyzed by the three static equations.  Beams with more than three  unknown reactions are considered  indeterminate and cannot be analyzed by the three  static equations alone.  A beam with two pin supports (1 has four unknown reactions, one  horizontal and one vertical reaction at each support.  Under load, in addition to bending,  this beam would deform like a suspended cable in tension, making the analysis more  complex and not possible with static equations.

By contrast, a beam with one pin and one roller support (2) has only three unknown  reactions, one horizontal and two vertical.  In bridge structures such supports are quite  common.  To simplify analysis, in building structures this type of support may be  assumed, since supporting walls or columns usually are    flexible enough to simulate the  same behavior as one pin and one roller support.  The diagrams at left show for each  support on top the physical conditions and below the symbolic abstraction.

1  Beam with fixed supports at both ends subject to bending and tension
2  Simple beam with one pin and one roller support subject to bending only
3  Beam with flexible supports, behaves like a simple beam

Simple beams, supported by one pin and one roller, are very common and easy to  analyze.  Designations of roller- and pin supports are used to describe the structural  behavior assumed for analysis, but do not always reflect the actual physical support.  For  example, a pin support is not an actual pin but a support that resists horizontal and  vertical movement but allows rotation.  Roller supports may consist of Teflon or similar  material of low friction that allows horizontal movement like a roller.

BRACED FRAMES - STRUCTURES

Braced frames resist gravity load in bending and axial compression, and lateral load in axial compression and tension by triangulation, much like trusses.  The triangulation results in greater stiffness, an advantage to resist wind load, but increases seismic  forces, a disadvantage to resist earthquakes.  Triangulation may take several  configurations, single diagonals, A-bracing, V-bracing, X-bracing, etc., considering both  architectural and structural criteria.  For example, location of doors may be effected by  bracing and impossible with X-bracing.  Structurally, a single diagonal brace is the  longest, which increases buckling tendency  under compression.  Also the number of  costly joints varies: two for single diagonals, three for A- and V-braces, and five joints for  X-braces.  The effect of bracing to resist load is visualized through amplified deformation  as follows:

1  Single diagonal portal under gravity and lateral loads
2  A-braced portal under gravity and lateral load
3  V-braced portal under gravity and lateral load
4  X-braced portal under gravity and lateral load
5  Braced frame building without and with lateral load

Note: deformations and forces reverse under reversed load

MOMENT FRAMES - STRUCTURES

Moment frames resist gravity and lateral load in bending and compression. They are derived from post-and beam portals with moment resisting beam to column connections (for convenience refered to as moment frames and moment joints).  The effect of moment joints is that load applied to the beam will rotate its ends and in turn rotate the attached columns.  Equally, load applied to columns will rotate their ends and in turn  rotate the beam.  This mutual interaction makes moment frames effective to resist lateral load with ductility. Ductility is the capacity to deform without breaking, a good property to resist earthquakes, resulting in smaller seismic forces than in shear walls and braced frames.  However, in areas with prevailing wind load, the greater stiffness of shear walls and braced frames is an advantage,  The effect of moment joints to resist loads is  visualized through amplified deformation as follows:

1  Portal with pin joints collapses under lateral load
2  Portal with moment joints at base under lateral load
3  Portal with moment beam/column joints under gravity load
4  Portal with moment beam/column joints under lateral load
5  Portal with all moment joints under gravity load
6  Portal with all moment joints under lateral load
7  High-rise moment frame under gravity load
8  Moment frame building under lateral load
I  Inflection points (zero bending between negative and positive bending

Note: deformations reverse under reversed load