1 Simple wood beam with hatched area and square marked for inquiry
2 Shear diagram with hatched area marked for inquiry
3 Bending moment diagram with hatched area marked for inquiry
4 Partial beam of length x, with stress blocks for bending fb and shear fv, where x is assumed a differential (very small) length
Reactions, found by equilibrium ΣM = 0 (clockwise +)
Shear V, found by vertical equilibrium, ΣV=0 (upward +).
Bending moment M, found by equilibrium ΣM=0 (clockwise +)
Bending stress fb is derived, referring to 4. Bending is resisted by the force couple C-T, with lever arm 2/3 d = distance between centroids of triangular stress blocks. C=T= fb bd/4, M= C(2d/3) = (fbbd/4)(2d/3) = fbbd^2/6, or fb= M/(bd^2/6); where bd^2/6 = S= Section Modulus for rectangular beam; thus
* multiplying by 1000 converts kips to pounds, by 12 converts feet to inches. Shear stress fv is derived, referring to 4. Bending stress blocks pushing and pulling in opposite directions create horizontal shear stress. The maximum shear stress is fv=C/bx, where b = width and x = length of resisting shear plane. Shear at left support is V = R.




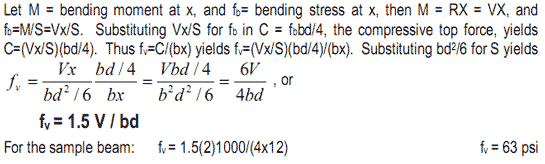

No comments:
Post a Comment